Chaturbate Recommends...

... someone with green hair, mismatched socks, precisely 3 black & gray tattoos, and butt freckles? Perhaps you fancy someone with excessively large glasses that role plays? Chaturbate wants to help viewers find those unique broadcasters that get them off while learning and suggesting more of them.  

Recommendation systems do what we need here: they filter products and predict user preferences. As a Chaturbate viewer, most interactions have a per-user experience catered to you. Flows like the tube, room listing, and next-cam take into account results from an internal service that has interchangeable recommendation algorithms.

The vast majority of recommender systems and literature about them focus on providing recommendations by modeling user preference as a single rating (like a movie rating). In scope for Chaturbate however, is the class of multi-criteria recommender systems that by nature capture user preferences along multiple dimensions.  Rather than predict an explicit, user-submitted, single rating of a broadcaster that the viewer has not seen, we instead opt for a multi-criteria score built from the implicit. We can consider tips, chats, followers, photo/video purchases, certain page events such as entering a room and clicking on a button, and viewing times.

Chaturbate understands that content filtering and matching systems do not always succeed in automatically matching content to one's preferences, so currently only a few user-specific recommendations are made and interspersed within results as user feedback and metrics are collected.

Methods

Chaturbate implemented a few variations on the standard major themes of Content-Based Filtering (personality-based) and Collaborative Filtering (multiple user based), each plugging into the recommender service interface for testing.

// algorithmselector.go
package algorithmselector

import ( ... )

var (
	algorithmName = flag.String("algorithm", "buckets", "Which algorithm should be used? buckets, svdcf ")
)

// CurrentAlgorithm returns the current algorithm.
func CurrentAlgorithm(db *db.DB) algorithm.Algorithm {
	switch *algorithmName {

	case "buckets":
		a := buckets.NewBucketAlgorithm(db)
		a.LoadDataFromDB()
		return a
	}
	case "svdcf":
		a := svdcf.NewSVDAlgorithm(db)
		a.LoadDataFromDB()
		return a
	}
	log.Panicln("Unknown algorithm:", *algorithmName)
	return nil
}

The current buckets approach does not require significant time or memory in the face of data sparsity. Nearest neighbor algorithms rely on exact matches that sacrifice coverage and accuracy; in particular, since the correlation coefficient is defined as a function between viewers who are interested in at least 2 broadcasters in common (cosine similarity between centered rating vectors), many pairs of customers have no correlation at all. Moreover, most active users will only have visited a small subset of the overall database, and their viewing times can drastically differ. With untweaked collaborative filtering, Chaturbate may recommend a broadcaster to user Bob due to user Charlie having similar browsing behavior, but Bob and Charlie may be in vastly different time zones. The recommendated broadcaster for Bob may never appear online when Bob wants to fap!

There is an additional challenge with matrix modeling. Having a user database of over 66 million people necessitates a large amount of computation power and memory unless reduced to a low rank approximation (O(k(n + d)) for an n x d matrix with rank k). This is alleviated by some filtering of time ranges and user activity.  This reduction is a huge win when k is relatively small and n and d are relatively large.  But how do you choose a value of k? If you choose a higher k, we get a closer approximation to the original matrix. On the other hand, choosing a smaller k will save on computation.  

Computing matrix factorization with SVD also requires the entries of the initial matrix to be fully populated– what do we prefill the other elements with?  The mean of row or column scores or 0?  The rule of thumb here from the Netflix competition is to do Stochastic Gradient Descent .

Chaturbate experimented with values of k=2 through k=100 for using the largest k singular values in doing a truncated SVD calculation, using a normalized score that is a combination of the multi-criteria factors called an SRow listed before in the original matrix, and by pre-filling the sparse matrix with a simple heuristic of the mean of the columns. The results were highly biased and still took significant computation.

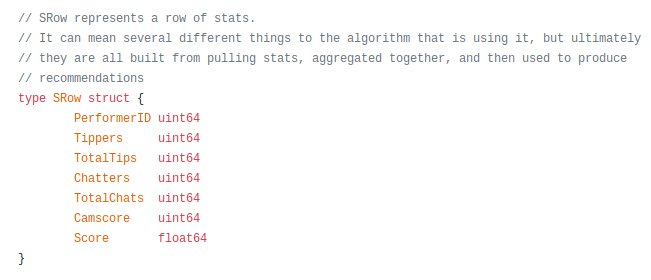
I won't list the exact formula for computing the normalized SRow.Score, but it is enough to know some influencing factors.

Bucket Algorithm

The Bucket Algorithm produces a score based on SRow factors for each viewer and broadcaster combination that the viewer has a history with. Unseen factors get tallied and are continuously marked for recalculation. If recommended results are enabled from the Chaturbate advanced settings, the viewer is displayed the broadcasters that map from the sorted list of buckets for the viewer.

Singular Value Decomposition (SVD)

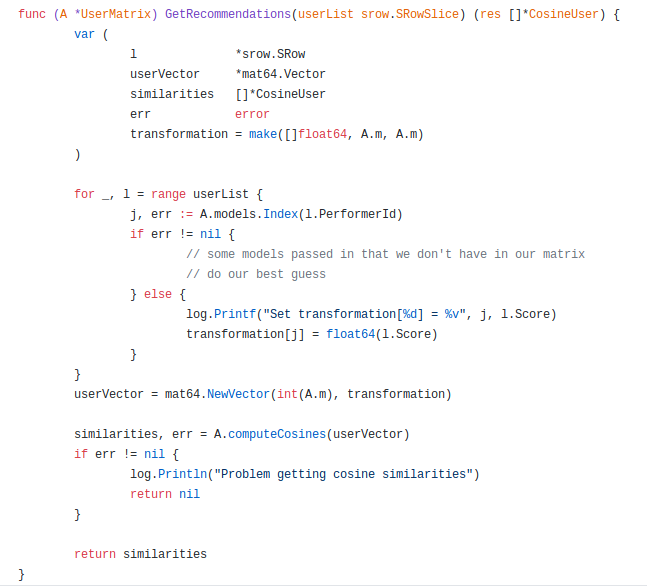
SVD was used with a low k-rank approximation on a model x viewer matrix with elements consisting of normalized SRow.Score values and then cosine similarities were computed between user vectors to return the highest matching broadcasters. We can say that for users Alice, Bob, and Charlie, each have a measure of closeness. The user vectors that have the closest similarity can have their highest scoring broadcasters returned back as recommendations.

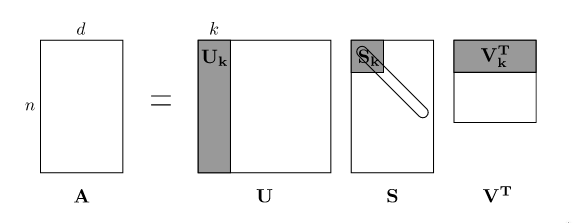
We saw earlier that rank-k approximations can be compared to determine an appropriate value of k. One trick is to calculate only the singular values of the original matrix by running svd(A), and you can plot the values in MATLAB or Mathematica with plot(svd(A)) . When you multiply the component U, S, and V back together, the larger singular values contribute more to the magnitude of A than the smaller ones.  

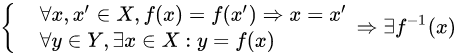
Results are returned for a user in the form of a vector of sorted similarity scores.

Summary

After filtering down to 30 days of activity and populating the original matrix with missing entries with the simple mean heuristic, the recommendations with the SVD approach took more computation time and were biased towards broadcasters that did not appear to be as good matches as what we found with the bucket approach. Currently the bucket algorithm is active.

Chaturbate is looking to hire competent people familar with these recommendation problems. If you are interested in working for us and in possibly plugging in a new algorithm, contact programmingjobs@chaturbate.com!